Olasılıklı Olan ve Olmayan Örneklemler

Eğer bir örneklemden yola çıkıp bir evren için genelleme yapmak istiyorsak, MLT’nin bizim için çalışmasını istiyorsak; örneklemin çekilme biçimi büyük önem taşıyor. Bizim kendi araştırmalarımızda kullandığımız örneklemler ya da her gün karşımıza çıkan araştırmaların örneklemleri eğer MLT’nin temel varsayımını yerine getirmiyorsa; o çalışmaların bulgularından çıkarım yapamayacağımız gibi, hata payı ve benzeri kavramlar da bizim için geçerli olmaz; çünkü o kavramlar MLT’nin geçerli olmasıyla yakından ilişkilidir.

Farklı örnekleme yöntemlerini olasılıklı ya da olasılıklı olmayan diye ikiye bölebiliriz. Olasılıklı yöntemler, evrendeki her birimin örnekleme dahil olma olasılığının hesaplanabildiği ve eşit olduğu yöntemler olarak tanımlanır. Basit bir örnekle başlayalım. Bir sınıfta 20 öğrenci var, beş kişilik bir örneklem çekmek istiyorsunuz. O zaman her bir öğrencinin bu örnekleme seçilme olasılığı 5/20, yani 1/4 olur. Bunu sağlamak için de rassal bir örneklem çekim yöntemi bulmanız gerekir.

Örneği genişletelim, diyelim 20 milyon seçmeni temsil edecek 1000 kişilik bir örnekleme ihtiyacınız var. O zaman her bir bireyin örnekleme seçilme olasılığı 1000/20.000.000 olması gerekir. Eğer bu olasılığı hesaplayamıyorsanız ya da hesapladığınız olasılıklar eşit değilse, örnekleme bir kayma olabilir, bu da yapacağımız çıkarımları şüpheli hale getirir.

Daha zor bir örnek düşünelim. Bizim yaptığımız gibi mevsimlik tarım işçileriyle bir anket yapmak istiyorsunuz. Evren büyüklüğünü bilmiyorsunuz, örneklem çerçeveniz tanımsız, yani elinizde mevsimlik tarım işçilerinin bir listesi yok. Öyle bir örneklem tasarlayacaksınız ki, her bir mevsimlik tarım işçisinin örneklemenize dahil olma olasılığı hesaplanabilir ve eşit olacak. Yoksa ne çıkarım yapabilirsiniz, ne de hata payı hesaplayabilirsiniz.

İşte bu tür bilgi ya da veri eksiklikleri başta olmak üzere, maliyet ya da zaman kısıtlılıkları gibi faktörler bizi kusurlu örneklemler tasarlamaya itiyor, sonuçta da geçerliliği sınırlı bulgular üzerinden tartışmalar yürütüyoruz. Ders kitapları hangi yöntemin doğru olduğunu şüphe içermeyecek şekilde anlatıyor, ancak sahadaki sınırlamalar bu ideal tasarımı her zaman sahada uygulamamızı mümkün kılmıyor.

Olasılıklı Olmayan Örneklemler:

Saydığımız kısıtlar ya da diğer sebeplerden dolayı yaygın bir biçimde olasılıklı olmayan örneklem yöntemlerinin kullanıldığını görüyoruz. Aslında hangi tür örnekleme yöntemlerinin olasılıklı, hangilerinin olasılıklı olmayan yöntem olduğunu örneklerle tartışmadan ayırt etmek de zor olabilir.

Gelişigüzel/Kolayda Örneklem

Bu örneklem türü, adından anlaşılacağı üzere araştırmacının işini son derece kolaylaştırır. Basitçe elinin altında bulunan kişilerden oluşan örneklemle araştırma yapmaya bu ad verilir. Bizim sınıflarımızda olan öğrencilerle anket yaptığımızı düşünün. Bu anketten kimler için çıkarım yapabiliriz? Sınıfımdaki öğrenciler kimi temsil eder?

• Türkiye gençliği?
• İstanbul’daki üniversite öğrencileri?
• İstanbul Bilgi Üniversitesi öğrencileri?
• İUluslararası İlişkiler Bölümü öğrencileri?
• Uluslararası İlişkiler Bölümü ikinci sınıf öğrencileri?
• Sosyal İstatistik Dersi öğrencileri?

Açıkça, anketimize katılan öğrenciler sadece kendilerini temsil ederler. Türkiye gençliği diye tanımladığımız o evrendeki her birimin, anketi yaptığımız anda, bizim sınıfımızda olma olasılığı bulunmuyor tabii ki. Aynı yanıtı İstanbul’daki üniversite öğrencileri için de verebiliriz, neden bizim sınıfımızda olsunlar ki? Kendi çalıştığımız üniversitede diğer fakülte, bölüm ya da sınıf öğrenciler de bizim sınıfımızda olamazlar, dolayısıyla örnekleme dahil olma olasılıkları yok. Bu dersi almayanlar da ankete katılamazlar. Pekiyi, sosyal istatistik dersi öğrencilerinin katılma olasılıkları var mı ve eşit mi? Kağıt üzerinde evet, ancak her öğrencinin her derse katılmadığı göz önünde tutulursa,  anket sonuçlarımızın o derse kayıtlı her öğrenciyi de temsil etmediği aşikar. O zaman baştaki yanıtımıza geri dönelim, anket sonuçlarımız sadece o ankete katılanları temsil eder, diğerleri hakkında çıkarım yapamayız.

Televizyon haberlerinde yapılan röportajları düşünün. Bu röportajlara herkesin katılma olasılığı var mı? Herkes o röportajların yapıldığı sokaktan o anda geçer mi? Geçse de herkesin kabul etme olasılığı denk mi? O zaman bu röportajların kimseyi temsil etmediğini bilelim.

Bazı televizyon programları seyircilere soru sorup SMS ya da benzeri yöntemlerle yanıt vermelerini istiyorlar. Yanıt verenler kimi temsil ediyor? Herkesin o anda o programı seyretme, o ankete katılma isteği duyma ya da o anketi yanıtlama olasılığı var mı?  Eşit mi? Tabii ki hayır. Sonuçta o anketler de sadece katılanları temsil ediyor.

Sosyal medyanın yaygınlaşmasıyla internet üzerinden yapılan bir anket türü yaygınlaştı.  Facebook ya da Twitter’da tek tuşla anket  hazırlayıp takipçilerinizi katılmaya davet  ediyorsunuz. Eğer takipçi sayınız yüksekse  binlerce kişinin katıldığı bir anket  yapabilirsiniz. Ünlü gurme Vedat Milor’un  “menemen soğanlı mı olur, soğansız mı?”  anketinde 437 bin kişi oy kullanmıştı. Bu  örneklem büyüklüğüne hiçbir araştırmada  rastlayamazsınız. Pekiyi, bu anket  sonuçlarını genelleyebilir miyiz, ya da kime genelleyebiliriz? Sadece Vedat Milor’un anketine katılanlar hakkında fikir verir, onların da kim olduğunu bilmiyoruz zaten.

“Bu kadar hatalı olduğu ya da genelleme yapılamayacağı açık olan bir yöntemi kim tercih eder ki” diyeceksiniz. Kâğıt üzerinde doğru. Ancak, her şehirde mutlaka bulunur, şehrin işlek caddesinde -İstanbul’da İstiklal Caddesi diyelim- bir grup anketör bulunur ve onlar gelen geçenlerle anket yaparlar. Sizce o anket kimi temsil eder? İstanbul seçmenleri mi? İstanbul’da yaşayan her seçmenin oradan geçme ve o ankete katılmaya kabul etme olasılığı var mı ve hesaplanabilir mi? Bazılarımız daha sık, bazılarımız daha seyrek geçeriz; bazılarımızın da ankete katılma olasılığı daha yüksek olur. Daha önce bahsettiğimiz Gallup’un anketörleri kadar akıllı anketörler, kimin anketi yapmayı kabul etme olasılığının daha yüksek olduğunu bilirler ve bu kişilere yaklaşırlar. Dolayısıyla bu yöntemde bu olasılığı hesaplamak imkânsız olur. İstanbul’un birçok yerinde bu anketörleri görebildiğiniz gibi, hemen her şehirde böyle bir anketör yoğunlaşmasının olduğu yerler bulunur, bu da bu yöntemin ne kadar yaygın olduğunu bize gösteriyor.

Gelişigüzel örnekleme yöntemini sadece gazeteciler, internet fenomenleri ve anket şirketleri kullanıyor, akademik araştırmalarda ne işi olabilir diyebilirsiniz. Oysa bu tür anket çalışmaları düşündüğünüzden çok yaygın olabilir. Psikoloji biliminde çalışmanın çoğunluğunun öğrenci örneklemlerinden geldiği biliniyor. Bir çalışmaya göre önde gelen psikoloji dergilerinde yayınlanan çalışmalara katılan deneklerin %68’i üniversite öğrencileri ve sıklıkla çalışmalara katılan psikoloji bölümlerindeki öğrencilerin toplumun geri kalanından çok farklı olduğu açık. Ayrıca çalışmaların %96’sı Batı ülkelerinde gerçekleştirilmiş, bu da çıkarımların ne kadar geçerli olduğunu tartışmaya açıyor.

Ülkemizde Suriyeli mültecilerin sayısının artmasıyla bu konudaki akademik ilginin arttığını biliyoruz. YÖK Tez Veritabanı’na göre şu ana kadar 600’den fazla yüksek lisans ya da doktora tezi yazılmış ve bu tezlerin %40’ında bir şekilde anket yapılmış. Anketlerin bir kısmı Suriyeli mültecilerle yapılırken, bir kısmı da Suriyeli ya da Türkiyeli öğrencilerle sınıflarda yapılmış. Üniversite öğrencileri de bu konudaki tezler için iyi birer bilgi kaynağı. Pekiyi bu örneklemlerden elde edilen bilgiler kimi temsil ediyor? Kimin için çıkarım yapabiliriz? Genelleme yapabilir miyiz? İşte bu soruları sorduğumuz zaman, ürettiğimiz bilginin niteliği hakkında açık bir yanıt almış oluyoruz.

Amaçlı Örneklem

Olasılıklı olmayan örneklem türlerinden biri de amaçlı örneklem. Gelişigüzel örneklemden farklı olarak bu örneklem türünde araştırmacı, belirli bir bölgeyi ya da mekânı kendi araştırma sorusuna uygun olarak “kasıtla” seçiyor, bu nedenle bu örneklem yöntemine “kasıtlı örneklem” ismi verildiği de olur. Bu araştırma türünde araştırmacı, kuramsal bilgisiyle ya da daha önceki deneyimiyle araştırma sorusuna en uygun vakaları ya da denekleri bulmaya ve araştırmasına dahil etmeye çalışır.

Diyelim Romanlarla ilgili bir araştırma çalışması yürütüyorsunuz. Bütün şehri tarayıp Romanları bulmanız mümkün değil, zaten Romanların sayısını ya da dağılımını bilmiyoruz. O zaman Romanların yoğun olarak yaşadığı mahallelere gitmek ve anketi orada yapmaya çalışmak çok daha kolay olabilir.

Suriyelilerle ilgili her çalışmada bu sorunla karşı karşıyayız, coğrafi dağılımları bilinmediği ve elimizdeki sayısal veriler eksik olduğundan dolayı, yoğun olarak yaşadıklarını bildiğimiz mahallelere giderek görüşmeleri gerçekleştirmek daha kolay gözükebilir.

Keza, LGBTİ+ bireylerle ilgili bir anket çalışmasında da katılımcıları tarama yöntemiyle bulmak mümkün değil. O zaman LGBTİ+ bireylerin daha çok bulunduğunu düşündüğümüz mahallelere ya da mekanlara gitmenin işimizi kolaylaştırdığını söyleyebiliriz.

Bu örnekleri çoğaltmak mümkün olabilir, örneğin “tipik bir çalışkan öğrencinin kütüphanede bulunacağı” varsayımından yola çıkarak, çalışkan öğrencilerle görüşmek için kütüphaneye gidebiliriz. Ya da fanatik futbol taraftarlarıyla ilgili bir çalışmada, onların kalabalık olduğu kafelere ya da tribünlere gidebiliriz. Bütün bu araştırma çabalarında hedeflediğimiz örnekleme alternatif yöntemlere kıyasla çok daha hızlı ulaşmamız mümkün olabilir, bu da bize kayda değer oranda zaman ve maddi kaynak tasarrufu sağlar.

Bu açılardan amaçlı örneklem yönteminin çok avantajlı olduğu kanısına kapılabiliriz. Öte yandan temsiliyet açısından çok kusurlu olduğu da açık. Bizim gitmeyi tercih ettiğimiz mahallede gerçekleştirdiğimiz anketler ne kadar temsili? Evrenimizdeki diğer aynı özellikteki kişilerin -Romanlar, Suriyeliler, LGBTİ+ bireyler ya da fanatik taraflar- bizim örneklemimize dahil olma olasılıkları var mı, bu olasılık hesaplanabiliyor mu ve eşit mi? Farkındayız örneklemimizi tasarlarken nerede daha sık rastlayacağımıza biz karar veriyoruz, bu aşamada önyargılarımızın seçimimizi etkilediği açık.

Bu tür örneklem tasarımlarının en önemli sakıncalarından biri, coğrafi yoğunlaşmaya yol açan diğer faktörlerin de etkili olabilmesi. Örneğin Suriyeli mültecilerle yürüttüğümüz bir çalışmayı düşünelim. En sık nerede rastlarız diye düşündüğümüzde aklımıza birden fazla mahalle gelebilir. Ancak, şunu da biliyoruz ki bütün Suriyeli mülteciler aynı mahallelerde oturmuyorlar, orada da neredeyse sınıfsal bir ayrım var. Daha fazla malvarlığına ya da ilişkilere sahip Suriyeliler daha müreffeh mahallelerde yaşamayı tercih ederken; daha kırılgan, daha yoksul olanlarsa “çöküntü” mahalleler adı verdiğimiz mahallelerde yaşıyorlar. İlk grubun sayısı daha az ve o mahallelerde “yerli nüfus” arasında kayboluyorlar ve göze çarpmıyorlar. İkinci grubun sayısı daha fazla ve yaşadıkları mahallelerde neredeyse nüfusun çoğunluğunu oluşturduğundan göze daha fazla çarpıyorlar. O zaman, bizim gitmeyi tercih ettiğimiz mahallelerde yaşayan Suriyeliler ile gitmediğimiz mahallelerde yaşayanlar arasında bizim araştırma sorumuzu doğrudan etkileyecek bir fark olamaz mı? Diyelim ki sosyal uyum konusunu çalışıyoruz. O zaman gittiğimiz en dezavantajlı mahallelerdeki kırılgan durumdaki Suriyelilerin mi sosyal uyum derecesi yüksek olur, gitmediğimiz mahallede yaşayanlar mı? Dolayısıyla istatistiksel anlamlılık taşımadığını biliyoruz zaten, ama bunu göze alsak da yaptığımız çıkarım eksik ya da kusurlu olmaz mı?

İşimizi ne kadar kolaylaştırsa kolaylaştırsın “amaçlı örneklem” hem temsili olmadığından hem de yapacağımız çıkarımların geçerliliği sorgulanabilir olduğundan, kullanılması tavsiye edilmeyen bir örneklem türü olarak bilinir.

Kartopu Örneklemi

Araştırma çalışmamız çerçevesinde erişmekte zorlanabileceğimiz bir hedef kitleyle yapacağımız çalışmalarda kullanabileceğimiz bir yöntem de kartopu örneklemi diye bilinir. Bu yönteme kartopu ismi verilmesinin sebebi, örneklemin tıpkı bir kartopu gibi birikerek büyümesi. Ulaşmayı hedeflediğimiz kitle sayıca az olabilir, örneklem çerçevesi bulunmaz ya da dağılımı bilinmez. Bu nedenle olasılıklı yöntemlerle erişmek çok maliyetli olabilir. Böyle durumlarda düzensiz göçmenler, mevsimlik tarım işçileri ya da yerinden zorla edilmiş kişiler gibi gruplarla çalışırken, bir temas noktasıyla başlayıp, onun tavsiyesiyle ikinci bir temas noktasına geçip bunu öngördüğümüz anket sayısına erişene kadar sürdürebilir ve anketi tamamlayabiliriz. Bu tür bir yürüyüş, sahada tarama yapmanın maliyetinden bizi kolayca kurtarır.

Öte yandan, eğer dışlanma, aile içi şiddet ve benzeri hassas konularda çalışıyorsak, olasılıklı bir örnekleme yöntemiyle çalıştığımızda hedef kitleye erişsek bile o kişilerin tanımadıkları kişilerle görüşmeleri ve hassas konuları paylaşmaları zor olabilir. Bu nedenle başlangıçta kurduğumuz güven ve tanışıklık ilişkisini diğer görüşmelere taşıyabilir ve çalışmamızı daha kolay, daha düşük ret oranları ve daha içten yanıtları alarak tamamlayabiliriz.

Bu tür bir yöntemin kolaylıkla erişemeyeceğimiz kişilere erişmemizi sağlaması, alternatif yöntemlere kıyasla daha düşük maliyetli olması ve daha kısa zamanda tamamlanması ve sabit bir planlama ihtiyacı duymadan, esnek bir biçimde yürütülebilmesi nedeniyle cazip olduğunu söyleyebiliriz. Özellikle de hassas gruplarla ya da konularda çalışırken erişemeyeceğimiz kişi ve bilgileri erişebilir kılması da diğer avantajları.

Bununla birlikte bu yöntemin de birçok dezavantajı olduğunu hatırlayalım. Öncelikle olasılıklı olmaması, istatistiksel anlamlılık testlerinin yapılmasını ya da bulgulardan istatistiksel çıkarım yapılmasını engelliyor. Elde ettiğimiz bulgular sadece görüştüğümüz kişileri temsil ediyor. Bu yöntemle bir dizi sokakta çalışan çocukla görüştüğünüzü düşünün. Bir tanesiyle tanıştınız, onu görüşmeye dahil ettiniz, görüşme sonunda bir ya da birden fazla arkadaşıyla iletişime geçirmesini istediniz. Diyelim ki yeterli bir sayıya ulaştınız ve araştırmayı durdurdunuz. Tam bu noktada aynı soruyu sormanız gerekiyor, o evrendeki her bir sokakta çalışan çocuğun sizin örnekleminize dahil olma olasılığı eşit miydi? Bu olasılık hepsi için var mıydı?

İkinci olarak başlangıç noktasında görüştüğünüz kişiden başlayarak, her temas noktasının sizi kime yönlendirdiğini bilemediğinizi kabul etmemiz gerek. Siz kendinizi ilk temas noktası olarak düşünün. Sizinle görüşen kişi, araştırmasına devam edebilmek için birkaç arkadaşınızın ismini istiyor. Siz hangi arkadaşlarınızın ismini verirsiniz? Tam bir çeşitlilik sağlamakla uğraşmayacağınız kesin, muhtemelen kabul etme olasılığı en yüksek olan arkadaşınıza yönlendireceksiniz ya da sizin açınızdan uygun olana. O kime ya da kimlere yönlendirecek?

Bir de araştırmanın grup kimliğinin etkisinin yüksek olduğu bir konuda yapıldığını düşünün. Sendikal hareketler üzerine bir araştırma yapıyorsunuz. Bir sendikada aktif olarak çalışan bir kişiyle ilk görüşmeyi yaptınız, sonra ondan iki arkadaşını önermesini istediniz. Sizce kime yönlendirir? Sendika üyesi olmak gibi bir kimlik söz konusu olduğunda sizi yönlendireceği kişi muhtemelen kimliği en iyi temsil eden üyeler olur. En azından görüştüğünüz kişi açısından böyle olduğunu düşündüğü kişilere sizi yönlendirir. Her aşamada bu şekilde bir yönlendirmeyle görüştüğünüz kişiler belirli özellikleri taşıyabilir. Örneğin, sendika içindeki en radikal üyeler olabilir, bu da sizin araştırma sonucunuzu hayli olumsuz etkiler.

Birazdan bahsedeceğimiz olasılıklı örnekleme yöntemlerinin uygulanamayacağı durumlarda, özellikle hassas gruplarla yürütülecek saha araştırmalarında hem amaçlı, hem de kartopu örneklemelerine başvurulması artık bir gelenek haline geldi. Ancak bu yöntemle derlenen verilerin istatistiksel genellemelerde kullanılamayacak olması önemli bir kısıt olarak ortadadır, bu kısıtın farkında olarak bulgular aktarılmalıdır.

Kotalı Örneklem

1936 seçimlerinin kazananı ve 1948 seçimlerinin mağlubu Gallup’ı hatırlayalım. Kendisi Amerikan seçmenlerini yaşadıkları eyalet, kır/kent, cinsiyet ve yaş ayrımında tasnif etmiş, her anketöre de bu dağılımda bir “kota” belirlemişti. Anketörler de bu kotalara uyan kişilerle görüşmüşler ve çalışmayı tamamlamışlardı. Ülkemizde de yaygın olarak kullanılan bu yöntem, kota yöntemi olarak bilinir ve olasılıklı olmayan örnekleme yöntemleri arasında sayılır.

Kota örnekleme yönteminde evren, elde bulunan çeşitli verilere göre tasnif edilir, yukarıdaki örnekte olduğu gibi yaş, cinsiyet ve kır/kent genel olarak kamuoyu araştırmalarında kullanılır. Daha sonra örneklem büyüklüğü bu kırılımlara, nüfuslarına orantılı olarak dağıtılır, böylelikle kotalar hesaplanmış olur. Bu kotaların doldurulmasıyla eldeki örneklemde her kırılım kendi büyüklüğüne orantılı olarak temsil edilmiş olur.

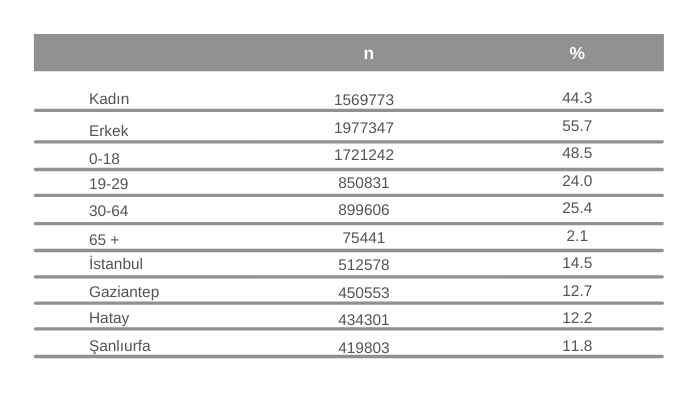
T.C. İçişleri Bakanlığı Göç İdaresi Genel Müdürlüğü'nün 17.03.2021 tarihli istatistiklerine göre Türkiye’de Geçici Koruma Statüsü altında yaşayan Suriyeli sayısı 3 milyon 663 bin 336. Kota örneklemi anlatma amacı ile yetişkinleri hedef almadan araştırmamızın evreninin bu olduğunu düşünelim. Yine aynı istatistiklere göre Suriyelilerin %44’ü kadın, %56’sı erkek. %49’u 18 yaş altında, %24’ü 19-29 yaş diliminde, 30-64 yaş arasında %25’lik bir kesim bulunurken, 65 yaş üstü olanların oranı %2. Aynı istatistikler bize bu evrenin %15’inin İstanbul, %13’ünün Gaziantep, %12’sinin Hatay yine %12’sinin Şanlıurfa ilinde yaşadığını söylüyor.

O zaman 1000 kişilik bir örneklemle Türkiye’de Geçici Koruma Statüsü altında yaşayan Suriyelileri temsil eden bir anket çalışmasında, kota örnekleme yöntemini tercih ederseniz, 1000 kişinin dağılımı da bu yüzdelere uymalı, yani 440 kadın, 560 erkek, 485 yaş altı çocukla görüşmeniz gerekir.  Anketlerin 145’i İstanbul, 127’si Gaziantep ve geri kalan da diğer illerde yapılmalı. Böylelikle kotaları belirlemiş oluyorsunuz.

Ancak böyle bir dağılım yeterince bilgi verici olmadığından, yaş ve cinsiyet gibi ortak dağılımları da belirlemek gerekir. Elimizdeki veriler bu hesaplamayı yapmamızı da sağlıyor. Aşağıdaki tabloda da görüldüğü üzere Suriyelilerin %26’sı 18 yaş erkek çocuk olduğundan, 1000 kişilik örneklemde 260 erkek çocuk bulunması gerekiyor. Örneklemde 228 kız çocuğu, 138 genç erkek, 102 genç kadın olması da aşağıdaki dağılımdan görülebiliyor. Eğer bu dağılımı tutturabilirseniz, bu çapraz dağılımdaki her hücreyi hakkıyla temsil etmiş olursunuz.

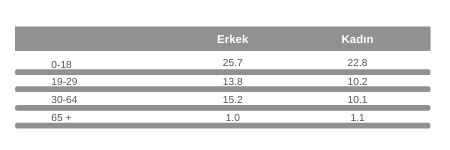
Tam burada resim karmaşıklaşıyor. İstanbul’da %14’lük bir kesimin yaşadığını biliyoruz. Pekiyi, 256 erkek çocuğun kaç tanesini İstanbul’da bulmamız gerekiyor. Resmî istatistiklerde bu dağılım yok. Eğer basit bir akıl yürütmeyle “eğer toplam evrenin %14’ü İstanbul’daysa, bu hücrenin de %14’ü İstanbul’da yaşıyor olmalı” derseniz, iki olayın (0-18 yaş dilimindeki erkek çocuk olmak ve İstanbul’da yaşamak) birbirinden bağımsız olduğunu varsaymaktasınız. Bu varsayım ne kadar doğru? 

Sosyal bilimlerde çoğu olay birbirine bağlı gerçekleşir. Bu durum bileşik olasılıkları hesaplamayı gerektirir ki bu neredeyse imkansızdır. Bağımsızlık varsayımı ise gerçekçi olmaz. Basit olasılık çarpımlarıyla elde edilen dağılımlar yanıltıcı olur. Kota örnekleminin amaçladığının tam aksine sonuç doğurarak, bazı grupların aşırı temsil edilmesine yol açabilir.

Kota örneklemiyle çalışıldığında, son örneklem noktasına kadar kotaları doğru hesaplayabildiğinizi varsaysanız bile, son örneklem noktasında görüşülecek kişiyi belirlemek çoğunlukla anketöre ya da onu denetleyen kişiye bırakılır. Bu da tıpkı Gallup’ın yaptığı hatanın yapılmasına, anketörlerin “durumlarına/keyiflerine göre” kişi seçmelerine yol açar. O zaman da, aynı soruyu sorduğumuzda, yani “herkesin bu örnekleme dahil olma olasılığı var mı?” diye sorduğumuzda, olumsuz yanıt alırız.  

Kota örneklemi ülkemizde yaygın biçimde kullanılır, hatta bazı kamuoyu araştırmalarında siyasi parti tercihinin de kota olarak kullanıldığı görülür. Bu tür bir uygulamanın yaygın olmasının çeşitli kurumsal ve kültürel nedenleri bulunuyor, ancak hesaplanamayacak hata paylarının verilmesi nedeniyle bu kullanım şekli bilimsel değildir. Yine de aşağıdaki örneklerde görüleceği üzere oldukça “bilimsel” bir görüntü yaratır ve yaygın olarak kullanılır.

Olasılıklı Örnekleme Yöntemleri

Daha önce de tartıştığımız üzere çoğunlukla başvurulan olasılıksız örnekleme yöntemleri istatistiksel çıkarıma izin vermemesi ve anlamlılık testleri yapılamayacağı için pek tercih edilen yöntemler değiller. Dolayısıyla MLT’nin bize sağladığı gücü kullanabilmemiz için, sahada uygulamakta zorlansak da, olasılıklı örnekleme yönemlerini tercih etmemiz daha doğru olur.

Basit Rassal Aşamalı Örnekleme

Olasılıklı örnekleme yöntemini uygulayabileceğimiz “ideal” dünyada, tercih etmemiz gereken yöntem, basit rassal örnekleme yöntemidir. Bu yöntemde evrenimizdeki bütün birimleri içeren tam bir örneklem çerçevemiz olduğunu varsayıyoruz. Diyelim ki, üniversitemizde bir anket yapacağız, evrenimiz bütün öğrenciler. Üniversitede olduğumuz için öğrencilerin tam bir listesine sahibiz. Basit rassal örnekleme yönteminde, bütün öğrencilerin isimlerini bir torbaya atıyoruz ve aralarından örneklem büyüklüğü kadar ismi çekiyoruz. Bu ideal durum.

Elinizde tam bir örneklem çerçevesi olduğu durumların hepsinde bunu yapabilirsiniz, yapmanız gereken tek şey aralarından kurayla seçmek. Eskiden istatistik kitaplarının eklerinde Rassal Sayılar Tablosu bulunurdu, ama şu anda çok daha hızlı biçimde bir bilgisayar programı kullanabilirsiniz ya da Excel’de bulunan “rand()” fonksiyonu çok işe yarar. Yine de akıldan uyduracağınız rakamların rassal olmayacağını her zaman hatırlamak gerekir.

Şekil 5.2 Basit Rassal Örnekleme

Sistematik Rassal Örnekleme

Basit rassal örnekleme en doğrusu olmakla birlikte, biraz zaman aldığı kesin. Bu nedenle geliştirilen sistematik rassal örnekleme denen bir yöntem basit rassal örneklemeyle aynı sonuçları üretebiliyor.

Bu örnekleme yönteminde adımlar şu şekilde ilerliyor, yine elinizde tam bir örneklem çerçevesi olduğunu varsayalım.

1. Evrenin toplam büyüklüğünü hesaplayın.
2. Örneklem büyüklüğünü hesaplayın.
3. Örneklemdeki her birimin temsil edeceği kişi sayısını hesaplayın:

F=N/n =Nüfus Büyüklüğü/Örneklem Büyüklüğü

4. 1 ile F arasında bir rakamı rassal olarak belirleyin, bu sizin ilk örneklem biriminiz olur.
5. İlk seçtiğiniz rakama F’i ekleyerek ilerleyin, denk gelen her birimi alın.
6. Böylelikle örnekleminiz çok hızlı bir şekilde çekilmiş olur.

Şekil 5.2 Sistematik Rassal Örnekleme

Görüldüğü üzere sistematik rassal örnekleme yöntemiyle çok hızlı bir şekilde rassal ve olasılıksal bir örneklem çekmiş oluyorsunuz. Öte yandan, tıpkı basit rassal örneklemde olduğu gibi, elinizde örnekleme çerçevenizin tam bir listesi olmadığı zaman, bu tür bir örneklem çekmek imkânsız olur.

Katmanlama

Gerçek hayatta örneklem tasarlarken tam bir örnekleme çerçevesini kullanmak yerine, hem temsiliyeti arttırmak hem de maliyeti azaltmak için farklı araçlar kullanıyoruz. Bunlardan ilk ele alacağımız  “katmanlama” (stratification).

Eğer evreninizi, sizi ilgilendiren herhangi bir kriter/değişken bazında gruplayıp "kendi içinde homojen" alt gruplar oluşturabiliyorsanız, bu tür bir katmanlama işlemini gerçekleştirdikten sonra örneklem çekmek, farklı grupları temsil edilmesini kolaylaştırır.

Örneğin üniversitemizdeki öğrencilerle anket çalışması yapacağız. Elimizde tam bir liste olmasına karşın, rassal bir örneklem hata payı içerisinde, örneklem büyüklüğüne bağlı olarak bazı fakültelerdeki öğrencilerin daha az, bazılarınınsa daha fazla temsil edilmesine yol açabilir. Bunu engellemek için, öğrencilerimizi fakültelere göre katmanlayabiliriz. Her bir katmanda kaç anket yapacağımızı hesapladıktan sonra, bu katmanlar içerisinde rassal yöntem ile örneklem çekebiliriz, böylelikle de her fakülte kendi nüfusu kadar temsil edilmiş olur. Buradaki önemli varsayım fakültelerin "kendi içlerinde homojen" katmanlar olması, eğer bu tür bir homojenlik yoksa, çok da büyük bir faydası olmaz.

Araştırma sorumuzla ilişkili olarak evrenimizi farklı şekilde katmanlamak mümkün olabilir. Kadına yönelik şiddet konusundaki algıları araştırıyorsak, kadın ve erkeklerin bu konuda kendi içlerinde homojen birer grup oluşturduğunu düşünebiliriz, o zaman cinsiyete göre katmanlamak mümkün olabilir. Siyasal katılımda, yaşanılan yerin kır ya da kent olmasının fark ettiğini düşünüyorsak, kentsel/kırsal ayrımı bir katman olabilir. 

Katmanlama yaptığınız bir evrenden örneklem çekerken karar vermeniz gereken şey, her katmanda ne kadar anket yapacağınız olur. Her katmanda eşit sayıda örneklem çekebilirsiniz, o zaman küçük katmanların fazla temsilini azaltmak için matematiksel bir işlem yapmanız gerekir. Eğer katmanlardaki örneklemleri nüfusa orantılı sayıda belirlerseniz, bu kez de küçük katmanlardaki anket sayınız az olacağından, katman bazında tahmin yapmanız zorlaşır. Bu konudaki kararınızı araştırma sorunuz ve katmanlarınızın yapısını göz önünde tutarak vermeniz gerekir.

Evreninizi katmanlayarak örneklem çekmek, eğer gerçekten katmanlar kendi içinde homojense hata payınızı azalttığı için çok avantajlı olabilir. Burada katmanlamanın kotalı örneklem ile karıştırıldığını görüyoruz. Kotalı örneklemde anketlerinizin ne kadarını kadınlar ya da erkeklerle yapacağınızı belirliyorsunuz, ama birimlerin nasıl seçileceğine müdahale etmiyorsunuz. Katmanlamada ise, her katmanda örneklemlerin büyüklüğü nüfusa orantılı ya da orantısız belirledikten sonra, her katmanda örnekleminizi rassal olarak seçtiğinizden emin oluyorsunuz, böylelikle MLT’nin sağladığı avantajdan yararlanabiliyorsunuz.

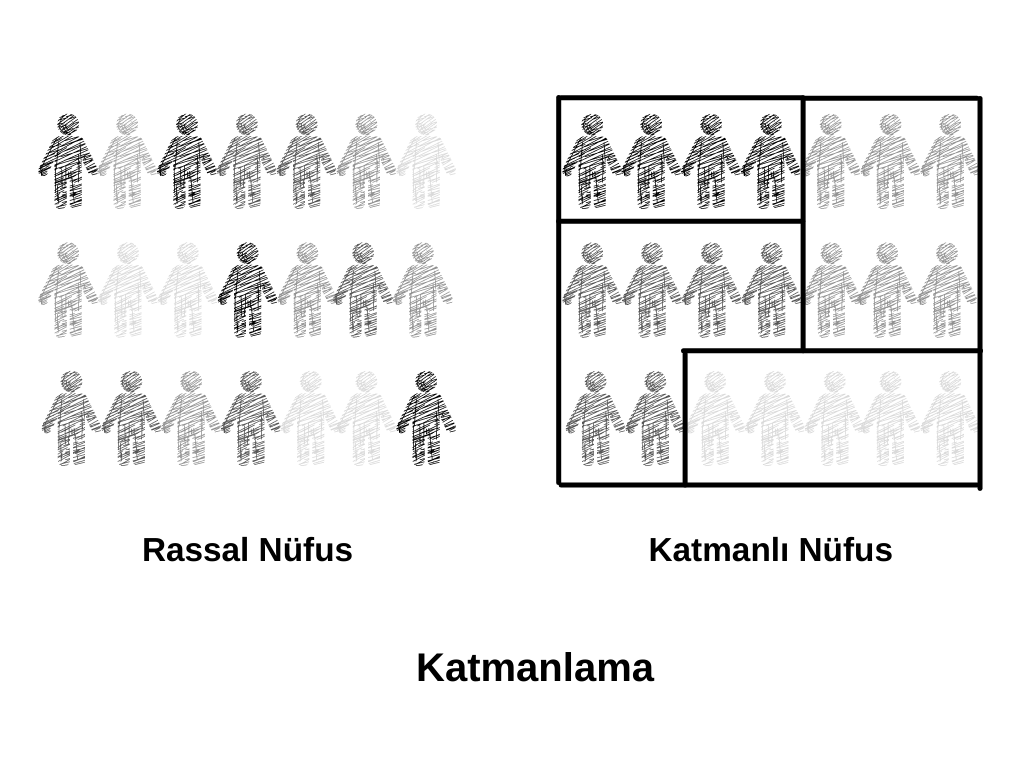
Şekil 5.3 Örneklem Belirleme için Katmanlama

Kümeleme

Örneklem tasarlarken kullanılabilecek araçlardan biri de "kümeleme" işlemi. Elimizdeki evreni, kendi içinde heterojen gruplara bölebiliyorsak, örneklemi kümelere ayırabiliyoruz. Böylelikle bütün örneklem içerisinden örneklem çekmek yerine, öncelikle kümeleri seçip, daha sonra kümeler içerisinden örneklem çekiyoruz, tabii ki rassal olarak. Kümeleme işlemi çok dağınık bir evren içerisinden görece yakın noktalara erişerek maliyet avantajı elde etmemize yarıyor, buna karşılık hata payını da arttırdığını biliyoruz. Burada maliyet ve hata payı büyüklüğü arasında tercih etmemiz gerekiyor.

Kümelemenin en tipik örneği anketlerde mahalleleri kullanmak. Diyelim şehrinizde bir anket çalışması yapacaksınız, çok şanslı olsanız bile 1000 kişilik bir örneklem şehrin her noktasına dağılır. Onun yerine mahalleleri küme olarak tanımlasanız, önce belirli bir sayıda mahalle seçip, daha sonra o mahalleler içerisinden görüşülecek kişileri belirleseniz, gideceğiniz mesafe hayli kısalır, zamandan ve maliyetten tasarruf edersiniz.

Evren içerisinde kümeleri belirlerken hepsi aynı büyüklükte olmayabilir. O zaman evrendeki her birime erişme olasılığı eşitlemek için "büyüklüğe orantılı olasılıkla örnekleme" adını verdiğimiz bir yönteme başvururuz. Bu yöntemde, daha büyük kümenin seçilme olasılığı, büyüklüğüne orantılı olarak daha yüksek olur. Örneğin X ilinin Y mahallesinin nüfusu 30 bin, Z mahallesininki bin. Eğer arada büyüklüğü gözetmez, ikisine de eşit şans verirsek, Z mahallesinde yaşayan birisinin seçilme olasılığı Y mahallesinin seçilme olasılığının 30 katı olduğundan, Z mahallesindekilerin “aşırı temsil” edilmiş olduğunu söyleyebiliriz. Böyle örneklem kaymasını engellemek için, büyüklüğe orantılı olasılıkla örnekleme yöntemiyle, Y mahallesinin seçilme olasılığını Z mahallesinin seçilme olasılığının 30 katı yapıyoruz ki, nihai örneklem biriminin seçilme olasılıkları eşit olsun.

Şekil 5.3 Kümeleme ile Örneklem Belirleme

Çok Aşamalı Örnekleme

Gerçek hayatta örneklemin içinde hem kritik grupların olmaları gerektiği kadar seçilme olasılığı vermek, hem de maliyetleri azaltmak amacıyla katmanlama ve kümelemeyi bir arada kullanarak daha etkin bir örnekleme yöntemi uygularız.

Üniversitemizde bulunan öğrencilerle yapmak istediğimiz anket çalışması üzerinden bu örneği genişletelim. Bizim üniversitemiz, İstanbul Bilgi Üniversitesi’nde 23000 öğrenci var. İdeal bir dünyada hepsini bir torbaya atar aralarından basit rassal örnekleme ile örneklem seçerdik. Ama zaman kısıtımız var, bu nedenle daha hızlı bir şekilde anketi tamamlamak istediğimizden çok aşamalı bir örnekleme tasarlamamız gerekiyor. Birlikte yürüyelim, diyelim ki araştırma konumuz gençlerin gelecekten umutları:

1. Üniversitemiz yedi fakülteden oluşuyor: Hukuk, İletişim, İşletme, Mimarlık, Mühendislik, Sağlık ve Sosyal ve Beşerî Bilimler. Araştırma sorumuz açısından bu fakülteler katman mı, küme mi? Eğer küme dersek, İletişim Fakültesi öğrencilerinin Mühendislik Fakültesi öğrencileriyle benzer bir şekilde dağıldığını söylemiş olacağız, oysa biliyoruz ki öyle değil. O yüzden fakülteler katman. Her fakültede nüfusuna uygun biçimde yapılacak anketleri dağıtacağız.
2. Fakülteler, bölümlerden oluşuyor. Sosyal ve Beşeri Bilimler Fakültesi’nin bölümleri arasında İngiliz Dili ve Edebiyatı, Karşılaştırmalı Edebiyat, Müzik, Psikoloji, Sosyoloji, Tarih ve Uluslararası İlişkiler var. Bu bölümler küme mi, katman mı? Araştırma sorumuz açısından düşündüğümüzde bu bölümler de katman, o yüzden her birine kendi nüfusuna uygun biçimde yapılacak anketleri dağıtıyoruz.
3.  Uluslararası İlişkiler Bölümü’ne odaklanalım. Bu bölüm sınıflardan oluşuyor, bu sınıflar küme mi katman mı? Başka bir deyişle gençlerin gelecekte umutları birinci sınıfta ve dördüncü sınıfta aynı şekilde mi dağılıyor? Bu soruya vereceğimiz yanıt da olumsuz olacağından, sınıfları katman olarak görebiliriz.
4. Sınıflar, derslerden oluşuyor. Her bir sınıf bir yılda yaklaşık 10 ders alıyor. Bu dersler küme mi, katman mı? Küme, çünkü dersler kendi içinde heterojen, kendi aralarında homojen. O zaman yapılması gereken sınıfların aldıkları dersler arasından mümkünse büyüklüğe orantılı olasılıksal biçimde ders seçmek, her dersi alanlar arasından 10 öğrenciyle anket yapmak.

Bu hesaplamayla, her dersten 10 öğrenci, her sınıftan iki ders, her bölümden dört sınıf, her fakülteden yedi bölüm hesaplamasıyla, toplam yedi fakültede 3920 öğrenciyle çok hızlı bir şekilde anket yapmamız mümkün. Tabii bu şekildeki örnek hesaplamada yukarıda 1,2,3 de belirttiğimiz sınıflar, bölümler ve fakülteler arasındaki öğrenci farkını işleme katmadan ilerledik. Aşağıda araştırmalarda kullanılmış olan çok aşamalı örnekleme örnekleri yer almakta:

Niteliksel Çalışmalarda Örneklem

Örneklem konusunda şu ana kadar yaptığımız tartışmalarda farklı örnekleme yöntemlerini tartışırken ana kriterimizin temsiliyet olduğunu hatırlayalım. Şu soruyu yanıtlamaya çalışıyoruz: “Çektiğimiz örneklem, hakkında çıkarım/genelleme yapacağımız evreni ne kadar temsil ediyor?” Eğer bu soruya olumlu bir yanıt veremiyorsak, örnekleme yöntemimizin sorunlu olduğunu söyleyebiliyoruz. Daha önce de aktarmaya çalıştığımız üzere bazı yöntemler daha temsili, bazıları daha az temsili, bazılarındaysa herhangi bir temsiliyetten bahsetmek bile mümkün değil.

Ancak asıl önemli noktalardan biri araştırma sorumuzla ilgili. Araştırma sorumuz çıkarım/genelleme yapmayı içeriyor mu? İçermiyor ise nasıl ilerlemek gerekir? Bilimsel araştırma çabasının temel amaçlarından birinin çıkarımlar yapmak ve böylelikle içinde yaşadığımız dünyadaki belirsizliği azaltmak olduğunu söyledik. Ancak, her araştırmanın amacı bu olmayabilir ve bu araştırmaların amaçlarının da en az diğerleri kadar bilimsel olduğunu söyleyebiliriz.

“Genelleme ya da genellememe” konusundaki tartışmayı daha çok niceliksel/niteliksel yöntem tartışmalarında görüyoruz. Niceliksel yöntemle çalıştığını söyleyen araştırmacılar için genelleme yapmak ya da nedensellikler keşfetmek çalışmaların ana hedefi, bunu hedeflemeyen ya da başaramayan çalışmaları yeteri kadar “bilimsel” görmeyebiliyorlar. Oysa, farklı yöntemler kullanan araştırmacılara ne tür bir amaçları olduğunu sorduğumuzda çok farklı yanıtlar alabiliyoruz.

Niceliksel ve niteliksel yöntem ayrımı üzerine olan tartışmayı ilerleyen konulara bırakıp, konumuz olan örnekleme yöntemleri bağlamında düşünelim. Eğer evrenin parametrelerini örneklem istatistiklerinden yola çıkıp belli bir hata payıyla tahmin etmek ya da eldeki hipotezleri test etmek gibi bir kaygımız yoksa, nasıl bir örnekleme yöntemi uygulamalıyız?

Özellikle detaylı olarak ele alacağımız derinlemesine görüşme ve odak grup bölümlerinde belirteceğimiz noktalar çerçevesinde örneklemi nasıl oluşturacağımızı tekrar ele alacağız. Her ne kadar birçok kaynakta yukarıda saymış olduğumuz olasılıklı örnekleme yöntemlerinin kullanılması tavsiye edilse de, niteliksel araştırmalarda bu tür örneklemeler uygulamak hem pek kolay olmaz, hem de gerek duyulmaz. Örnekleme yönteminin rassal olması gerekliliği MLT’nin çalışabilmesi için gerekir, MLT’ye ihtiyacınız yoksa, rassal olmayan örnekleme yöntemlerini de meşru olarak kullanabilirsiniz.

MLT’nin varsayımlarına uymak zorunda olmamak, araştırmacıya büyük bir özgürlük hissi verebilir, yukarıda tarif edilen çok karmaşık süreçleri takip etmek gerekmez. Ancak bu da niteliksel araştırmaların “örneklemsiz” olması anlamına gelmemelidir. Nitel araştırmaların başarılı olmasını sağlayan en önemli noktalardan biri örneklemin ne kadar iyi oluşturulduğudur. Bu çerçevede araştırma sorusuna istinaden yapılan evren tanımı, örnekleme çerçevesi ve örnekleme yöntemi kapsamlı bir biçimde ele alınarak belirlenmelidir. 

Niteliksel araştırma yapanlarda yaygın olarak kullanılan yöntem “gelişigüzel/kolayda” olsa da, bu tür bir örnekleme yönteminin sağlıklı olmadığı ve araştırmacıyı yanlış yönlendirdiğini hatırlayalım. Gelişigüzel örnekleme yöntemiyle erişebileceğimiz kişiler -öğrenciler, arkadaşlar, akrabalar vs.- bize gerçekliğin yanlı bir temsilini verirler, sonuçta da yukarıdaki sorulardan hangisini yanıtlamak istersek isteyelim, yanıltıcı sonuçlara varırız. O yüzden araştırmacının kendisine bir örnekleme çerçevesi oluşturması ve orada yer alan her bir vakanın/kişinin neden dahil edildiğini açıklayabilmesi gerekir.

Şuradan başlayalım, niteliksel araştırmalarda örneklem yöntemi ne olursa olsun “amaçlı” olarak tanımlanır, buna “seçici” de diyebiliriz. Araştırmacı örneklemine dahil edeceği kişileri kuramsal kaygılarla ya da zaman, mekan ya da güç ilişkileri gibi bazı boyutlar üzerinden belirleyebilir. Araştırma sürecindeki deneyimi bazı yeni vakaları dahil edip, bazılarını da dışarıda bırakmasına yol açabilir, bütün bunları da bilinçli bir tercih sonucunda yapması beklenir.

Patton (1990, 2002) niteliksel araştırmalarda kullanılabilecek 9 farklı örnekleme yöntemi listeler, bunların hepsini de amaçlı örnekleme yöntemi olarak tanımlamak mümkün. Patton’a göre öncelikle bir karar vermek gerekir, örneklemde benzerlik mi arıyoruz, yoksa farklılık mı? Elimizdeki vakalar birbirine benzerlik mi taşımalı yoksa olabildiğince çok farklı seslere yer mi vermeliyiz?

Örnekleminizde benzerliklerin önem taşıması gerektiğini düşünüyorsanız, başvurabileceğiniz amaçlı örnekleme yöntemlerini şöyle listeyebiliriz:

• Önemliler: Belirleyeceğiniz bir kritere göre, araştırma sorunuz için en önemli vakaları incelemek isteyebilirsiniz. Bu önem kriteri dışsal da belirlenmiş olabilir -en başarılı öğrenciler/ayakkabı sektöründe üç yıldır çalışan çocuk işçiler - ya da siz kendiniz bu kriteri belirleyebilirsiniz, bir coğrafyadaki en önemli siyasi aktörler;
• İstisnalar: Yine önceden belirlenmiş bir kritere göre, bu kriterin dışında kalan istisnalara odaklanabilirsiniz -en başarısız öğrenciler/ayakkabı sektöründe çocuk işçi olarak bu ay işe başlayanlar- ya da kendiniz bir kriter belirleyebilirsiniz, bir coğrafyadaki siyasal örgütlenmenin en önemsiz üyeleri.
• Tipik Örnekler: Araştırmayı hedeflediğiniz evrenin en tipik örneğini araştırabilirsiniz: Tipik ev kadını, tipik mevsimlik tarım işçi. Burada amaç genellikle alanın dışından gelenlere tipik/ortalama bir vakanın nasıl olduğunu anlatmak amacıyla örneklem oluşturulur.
• Homojen Gruplar: Araştırma evreninizi homojen alt gruplara -katmanlara- bölerek bu gruplardan birine ya da bir kaçına odaklanabilirsiniz. Örneğin göçmenlere odaklanırken,  Suriyeli göçmenler, Afgan göçmenler ya da Afrikalı göçmenler gibi farklı alt gruplardan birine hatta onun da alt kümesi örneğin Suriyeli kadın göçmenlere odaklanmak olabilir.
• İstisnai Örnekler: Araştırma konunuzda öngördüğünüz durumun dışında kalan istisnalara yönelebilirsiniz. Eğitim ile siyasal katılım arasında doğrusal bir ilişki beklerken, çok yüksek eğitimli ancak siyasetle ilgisiz bir kişi bu tür bir örnek sayılabilir. Mevsimlik tarım sürecinde ailesi ile farklı illere giden ama yine de okula devamı aksatmayan, başarı ile okula devam eden çocuklarla görüşmek de başka bir örnektir.   
• Kartopu Örneklemi: Daha önceden tanıdığımız bu yöntemde ilgilendiğimiz grubun “tipik” bir örneğiyle çalışmaya başlar, buradan ona benzer diğer örneklere yönelebiliriz. Kartopu örnekleminin bilindik sakıncası olan gittikçe homojenleşme, burada bir avantaj halini alır.

Eğer örnekleminizi oluştururken, farklılıklara odaklanacağınız bir örnekleme yöntemi takip etmek isterseniz, alternatifler şunlar olabilir:

• Yoğunluk Örneklemi: İstisnai örneklerle çalışmaya benzer, ancak bu kez iki aşırı uçtan olabildiğince görüşme yapar, farklılıkları keşfetmeye çalışırsınız: Çok başarılı ve çok başarısız öğrencilerle görüşmeler yapmak böyle bir strateji sayılır.
• Maksimum Farklılık: Burada örnekleminizin ilgilendiğiniz konudaki bazı boyutlarda maksimum farklılık taşıyan şekilde oluşmasını sağlarsanız, örneğin cinsiyet, yaş, yerleşim, siyasi tercih gibi. Bu kadar farklı özelliklere rağmen aynı sonuç gözlemleniyorsa, bulgularınız ilginç olabilir.
• Kritik Vaka: İlgilendiğiniz konudaki bütün önemli özellikleri taşıyan bir vakaya odaklanırsınız, bu özellikleri daha az taşıyan diğer vakaların bu kritik vakaya benzeyeceğini umarsınız.

Saydığımız örnekleme yöntemlerine “kuram bazlı” örnekleme adı verilen bir başka yöntemi de ekleyebiliriz. Özellikle “temellendirilmiş kuram” (grounded theory) çalışan sosyal bilimcilerin tercih ettiği bu yöntemde hangi vakaların önemli olduğunu araştırmanızın kuramsal çerçevesi size kendiliğinden söyler, bu vakalara odaklanmak gerekir. Örneğin mültecilerin sahip olduğu sosyal sermayenin onların sosyal uyum derecesini belirlediğini söyleyen bir kuramsal çerçeveden yola çıkmışsak, hedeflememiz gereken sosyal sermayesi ve sosyal uyum derecesi yüksek mültecilerle görüşmektir.

Bu örneklem ile çalışırken, karşımıza çıkacak istisnai vaka, sosyal sermayesi yüksek olduğu halde sosyal uyum derecesi düşük olan bir mülteci örneği bizim kuramımızı zenginleştirmemizi sağlar. İlk başta tümevarımsal gibi gözüken bu yöntem, vakalardan kuram üretmeyi amaçlayan “temellendirilmiş kuram” perspektifinden sorunlu sayılmaz. Bu yöntemin amacı “genellemek değil, yeniden inşa etmek” olarak tanımlandığından, kuramı zenginleştirecek istisnai vakalar ilgi çekici olur.

Başka bir yöntem de “mütekaip/ardıl örneklem” (sequential sampling). Görüştüğünüz birinci vaka ya da erken vakalar, araştırmacıya yanıtlaması gereken yeni sorular verebilir. Dolayısıyla bir sonraki vaka seçimi bu sorular çerçevesinde yapılabilir. Diyelim ki sosyal sermayesi yüksek mültecilerle yaptığımız görüşmeler, etnik ya da mezhepsel ayrımların da önemli olduğuna dair ipuçları verdi. O zaman bir sonraki görüşmemizi, ilk görüştüğümüz vakadan farklı bir etnisiteye/mezhepe sahip bir kişiyle gerçekleştirebiliriz ve bu görüşmelere devam edebiliriz. Tabii ki burada seçim sürecinin belgelenmesi gerekir, yoksa araştırma çalışmasının raporlanmasında örneklemin nasıl oluştuğuna dair bir belgeleme yapamayız.